La topología es una rama relativamente joven de las matemáticas, con varias ramas propias. Tiene aplicaciones en biología, informática, teoría de cuerdas y sí, también en cartografía. El mapa topológico de Europa de este topólogo no es un fiel reflejo del área o el tamaño, solo de las relaciones entre países.
Aquí hay una ología de la que quizás no haya oído hablar, a pesar de su nombre que suena engañosamente familiar: topología . Y si es así, bien hecho. Pero incluso entonces, probablemente nunca hayas considerado sus implicaciones cartográficas.
La topología es el estudio matemático de las propiedades que conservan los objetos incluso cuando se deforman, tuercen y estiran, pero no se rompen ni se pegan. Debido a todas esas torsiones y estiramientos, la topología a menudo también se denomina «geometría de hoja de goma».
Por ejemplo, dado que un círculo se puede estirar hasta una elipse, esto significa que ambos objetos son topológicamente equivalentes. Lo mismo se aplica en el espacio tridimensional: una esfera se puede estirar en un elipsoide, por lo que ambos son topológicamente equivalentes.
Para aclarar aún más, un contraejemplo: una figura 8 no se puede deformar en un círculo sin ‘romperlo’, por lo que ambos objetos no son topológicamente equivalentes.
La maleabilidad teórica de un objeto a otro que la topología presupone está en la base del primer chiste sobre topología que haya escuchado y el último que necesitará.
P: ¿Qué es un topólogo?
R: Alguien que no puede distinguir entre una dona y una taza de café.
(plantas rodadoras)
Todo esto parece un poco inútil, entonces, ¿para qué sirve realmente la topología ? El punto es que algunos problemas geométricos no dependen de la forma de los objetos involucrados, sino de la forma en que se ensamblan.
Este problema surgió por primera vez a mediados del siglo XVIII, en el llamado «problema de los siete puentes» de Leonhard Euler (ver también #536). Euler demostró que no se puede dar la vuelta a Königsberg usando todos sus puentes una sola vez, pero esto no tiene nada que ver con sus propiedades inherentes; sólo con la forma en que fueron colocados.
A pesar de ser una rama relativamente joven de las matemáticas, la topología solo despegó a principios del siglo XX, ya ha brotado varias ramas propias, incluida la topología general, algebraica y diferencial.
La topología también tiene una amplia variedad de aplicaciones: informa el estudio de nanoestructuras biológicas, es relevante para la programación de computadoras, sirve como herramienta para los teóricos de cuerdas e incluso se usa para describir la forma misma del universo (en lo que se llama espacio-tiempo).
Afortunadamente, la intersección de la topología y la cartografía implica mucha menos ciencia espacial. En pocas palabras, un mapa topológico es un diagrama del que se han eliminado detalles innecesarios para que solo se muestre la relación entre los distintos puntos.
Quizás el ejemplo más famoso es el mapa esquemático del metro de Londres, que representa la red de estaciones de metro con la simplicidad de una red eléctrica, ignorando la distancia real y las rutas entre las estaciones, mostrando solo cómo se interconectan. (Ver también #119). Esa representación ahora se ha convertido en un estándar global para los mapas de metro.
Peter Staub es un ingeniero de datos espaciales y un experto en mapas que ha llevado la topología a la superficie. Recientemente elaboró este Mapa Topológico de Europa, y es una delicia.
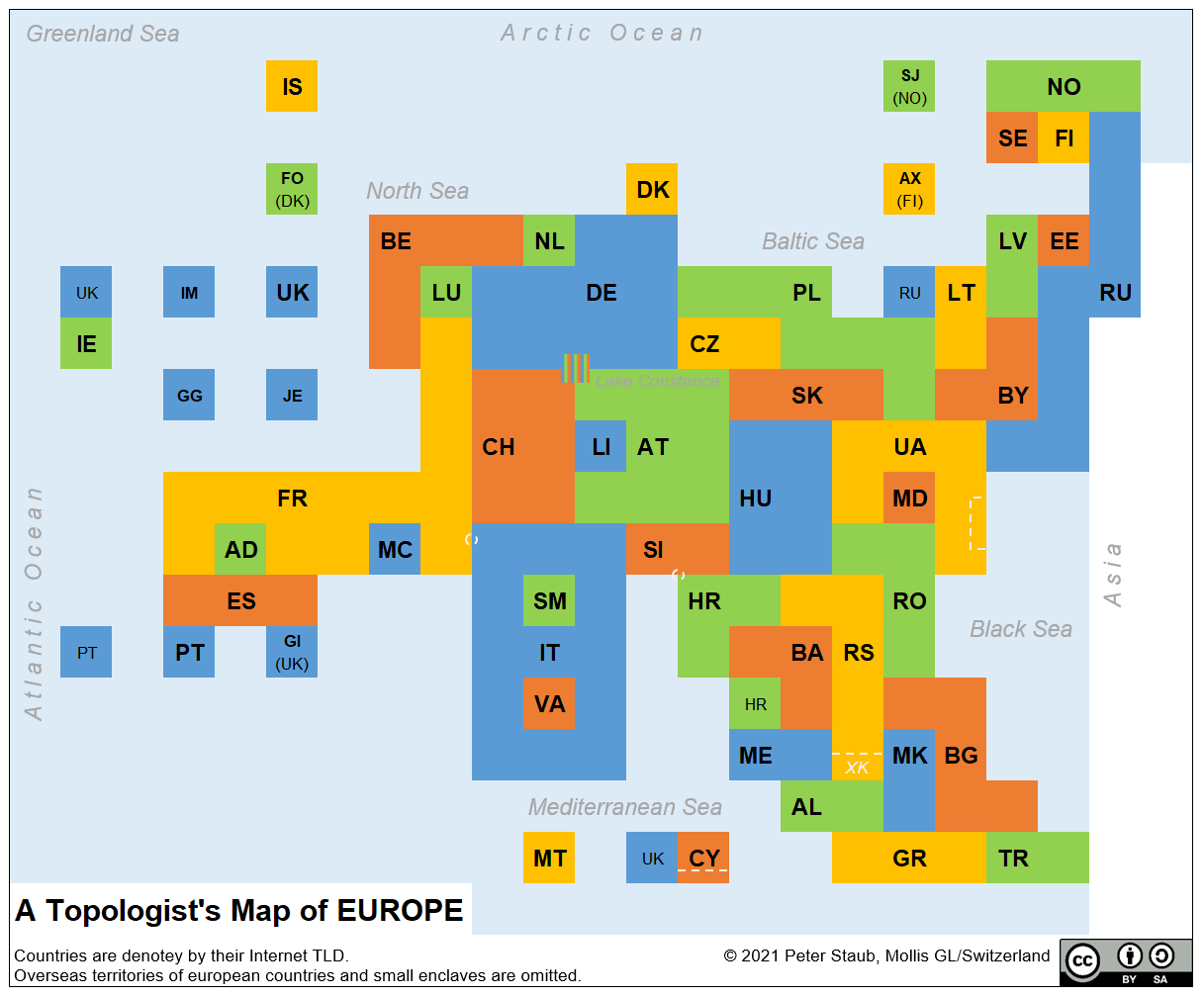
Según la definición anterior, este mapa topológico es un diagrama del que se han eliminado todos los detalles, excepto la relación espacial entre los distintos países. Entonces vemos exactamente con qué otros países limitan. Para mostrar esas relaciones, se han sacrificado totalmente las formas y tamaños reales de los países.
Tomemos Italia, por ejemplo: con forma de bota en cualquier mapa normal, aquí el país se parece a la figura 8, para acomodar a los dos países enclavados en su interior: el Vaticano y San Marino.
Polonia todavía limita con Alemania, la República Checa, Eslovaquia, Ucrania, Bielorrusia, Lituania y el enclave ruso de Kaliningrado, como lo hace en la vida real; pero para ello, el país ha tenido que pasar de ser un bloque a ser un garabato.
Francia ahora parece una silla de fondo largo con Andorra y Mónaco entre las piernas y Bélgica como reposacabezas.
Los países se indican por sus TLD de Internet (nombres de dominio de nivel superior). Algunos de los menos familiares son Isla de Man (IM), Jersey (JE) y Guernsey (GG), todas dependencias de la Corona británica.
El mapa también refleja minuciosamente las disputas territoriales más controvertidas de Europa, de ahí las líneas punteadas en Chipre (para la república separatista casi universalmente no reconocida del norte de Chipre) y en Ucrania (supuestamente para la anexión unilateral de Crimea por parte de Rusia, o son estas las áreas separatistas en el este ¿controlado por rebeldes prorrusos?)
Las pequeñas áreas punteadas indican disputas entre Eslovenia y Croacia, y entre Francia e Italia (sobre si la frontera entre ellos cruza la cima del Mont Blanc o no).
Kosovo es reconocido por muchos países, pero aún no por Serbia, de la que se separó. No tiene su propio bloque, pero su TLD (XK) se menciona debajo de la línea de puntos.
¿Y qué pasa con esa pequeña área entre Alemania (DE), Suiza (CH) y Austria (AT) que parece que hay algún problema con su televisor? Ese es el lago de Constanza, en la frontera entre Alemania, Suiza y Austria. Según Suiza, la frontera pasa justo por el medio del lago. Austria afirma que todo el lago es un condominio entre los tres países y la posición de Alemania es ambigua.
Como tal, el lago de Constanza es la única zona de Europa donde los estados vecinos nunca han logrado ponerse de acuerdo sobre una frontera. Ahora, eso es algo que no habrías aprendido si no fuera un mapa topológico.